Softmax to Gibbs

The Subtle Magic of Softmax: Unveiling the Gibbs Distribution

Disclaimer : I am not a physicist.

It’s funny how often we use softmax without realizing we’re invoking a physical principle from statistical mechanics. But here’s the kicker: when we softmax our logits, we’re actually sampling from a Gibbs distribution. Now, why should you care? Let me break it down:

Maximum Entropy Principle: The Gibbs distribution isn’t arbitrary - it’s what you get when you maximize entropy subject to energy constraints.
Temperature Control: Remember that temperature parameter $T$ in the Gibbs formula? It’s usually set to 1 and forgotten. But by exposing it, we get a knob to tune the “decisiveness” of our model. Low T? Sharp decisions. High T? More exploration. It’s like having a built-in simulated annealing mechanism.

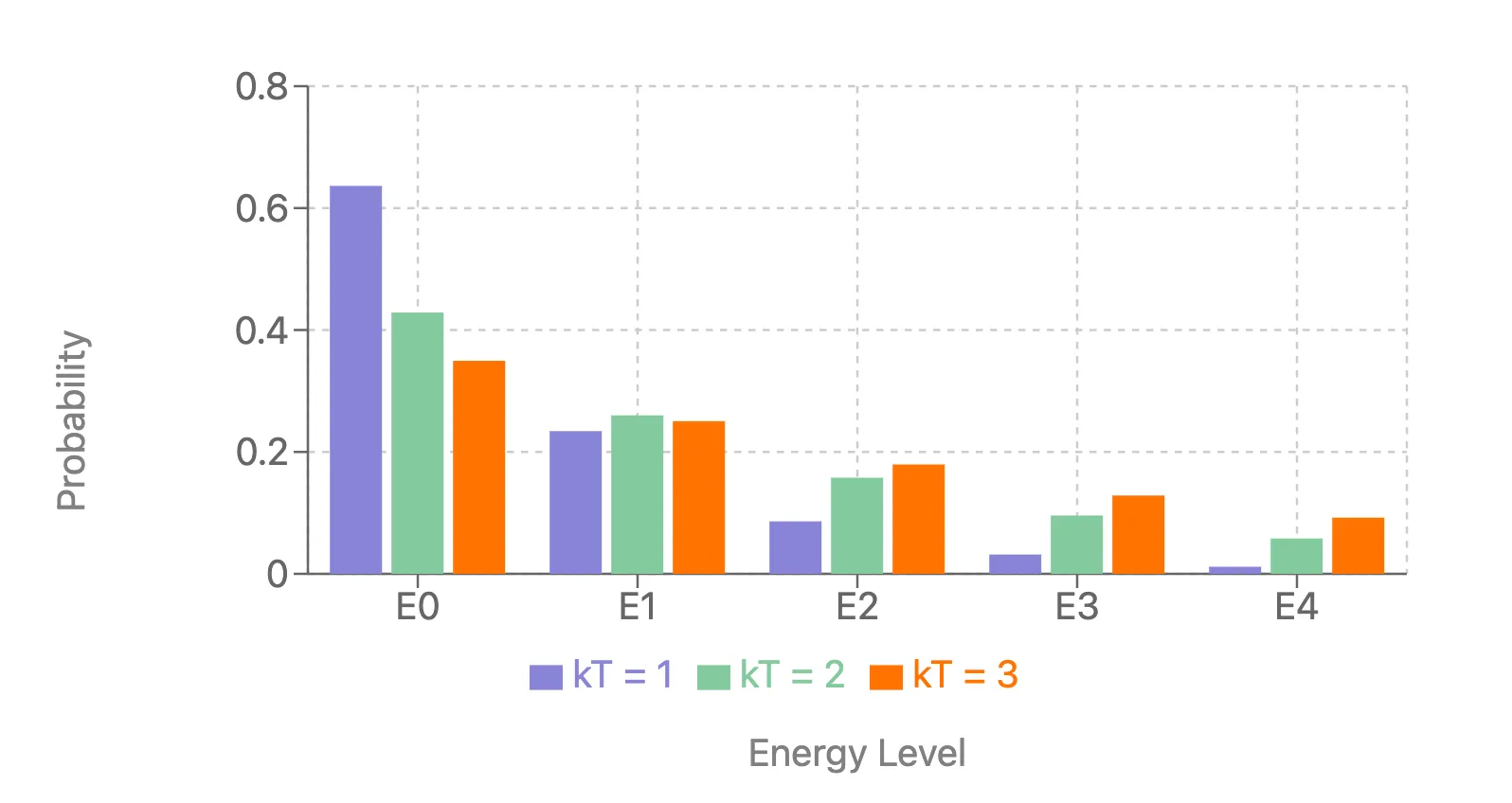
Temperature Control

Bridge to Physics: Recognizing the Gibbs distribution opens a two-way street between machine learning and statistical physics. We can borrow ideas from physics (like mean field theory) and potentially contribute back.

Let me convince you that Gibbs distribution is actually, is the one with the max entropy.

System States

Consider a system that can exist in a discrete set of states labeled by $i$ . Each state $i$ has an energy $E_i$ .

Probabilities

Let $P_i$ be the probability of the system being in state $i$ .

Then, the entropy $S$ of the system is given by:

S = -k \sum_i P_i \ln P_i

where $k$ is Boltzmann’s constant.

Constraints

The sum of all probabilities must equal 1.

\sum_i P_i = 1

The average energy $\langle E \rangle$ of the system is fixed.

\sum_i P_i E_i = \langle E \rangle

Lets maximize the entropy $S$ with respect to the probabilities $\{P_i\}$ while satisfying the two constraints.

We are going to use Lagrange multipliers $\alpha$ and $\beta$ to incorporate the constraints into the optimization.

Lagrangian Function

L = -k \sum_i P_i \ln P_i - \alpha \left( \sum_i P_i - 1 \right) - \beta \left( \sum_i P_i E_i - \langle E \rangle \right)

We need to find the probabilities $P_i$ that maximize $L$ . So we simply take the partial derivative of $L$ with respect to each $P_i$ and set it to zero:

\frac{\partial L}{\partial P_i} = 0

\frac{\partial L}{\partial P_i} = -k \left( \ln P_i + 1 \right) - \alpha - \beta E_i

-k \left( \ln P_i + 1 \right) - \alpha - \beta E_i = 0

Rewriting the equation,

-k \left( \ln P_i + 1 \right) = \alpha + \beta E_i

Divide both sides by $-k$ ,

\ln P_i + 1 = -\frac{\alpha}{k} - \frac{\beta}{k} E_i

\ln P_i = -1 - \frac{\alpha}{k} - \frac{\beta}{k} E_i

Exponentiate both sides to solve for $P_i$ ,

P_i = e^{-1 - \frac{\alpha}{k}} e^{-\frac{\beta}{k} E_i}

Define a constant $A$ ,

A = e^{-1 - \frac{\alpha}{k}}

So,

P_i = A e^{-\frac{\beta}{k} E_i}

Use the normalization constraint to solve for $A$ :

\sum_i P_i = \sum_i A e^{-\frac{\beta}{k} E_i} = 1

Therefore,

A = \frac{1}{\sum_i e^{-\frac{\beta}{k} E_i}} = \frac{1}{Z}

where $Z$ is the partition function:

Z = \sum_i e^{-\frac{\beta}{k} E_i}

Substitute $A = \frac{1}{Z}$ back into the expression for $P_i$ :

P_i = \frac{e^{-\frac{\beta}{k} E_i}}{Z}

This is the Gibbs (Boltzmann) distribution.

Relationship Between $\beta$ and Temperature

In thermodynamics, the Lagrange multiplier $\beta$ associated with the energy constraint is related to the inverse temperature. Specifically:

\frac{\beta}{k} = \frac{1}{k T}

So,

\beta = \frac{1}{T}

Substitute back into the expression for $P_i$ and $Z$ :

P_i = \frac{e^{-E_i / k T}}{Z}

And

Z = \sum_i e^{-E_i / k T}

By maximizing the entropy $S$ with respect to the probabilities $P_i$ under the constraints of normalization and fixed average energy, we derive the Gibbs distribution:

P_i = \frac{e^{-E_i / k T}}{\sum_j e^{-E_j / k T}}