Gumbel-Max Trick

Gumbel-Max Trick

Gumbel-Max trick is a pretty interesting way of easily sampling from a pmf which is defined by the logits(and their softmaxed versions, individual probabilities). It also influenced subsequent research in deep learning which I will touch upon. The trick goes like this: Say you have logits at the final layer of a neural network and you want to convert those logits to probabilities - naturally, by softmaxing them- and want to sample from that resulting pmf. You can achieve this by adding Gumbel Noise to each logit and take the $argmax$ of the resulting vector.

1. Add Gumbel noise to logits: For each alternative, draw a random number from a Gumbel distribution and add it to the corresponding logit:

2. Select the maximum: The alternative with the highest perturbed utility $z_i$ is selected:

   $$i^* = \arg \max_i z_i$$

This process guarantees that the choice is sampled according to the softmax probabilities:

Note that to implement the Gumbel-Max trick correctly, you should sample from the standard Gumbel distribution with location $\mu = 0$ and scale $\beta = 1$

Proof

In this blog post, I go over the mathematical proof pretty rigorously. So here, I will do what I would normally do when I see this kind of stuff online: just verify it by code.

Suppose we have logits:

$V = \left[ 2, 0.5, 0.5, 1 0.3 \right]$

These logits correspond to following pmf when we softmax them: $P(i) = \frac{\exp(V_i)}{\sum_{j} \exp(V_j)}$

$pmf = \left[0.50, \quad 0.11, \quad 0.11, \quad 0.18, \quad 0.09 \right]$

I will implement the gumbel-max trick and verify that we are actually sampling from this pmf. Lets start by importing the required libraries and setting the seed.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.special import softmax

# Set random seed for reproducibility
np.random.seed(42)

Lets implement three functions:

1. sample_gumbel creates gumbel noise

def sample_gumbel(shape, eps=1e-20):
    U = np.random.uniform(0, 1, shape)
    return -np.log(-np.log(U + eps) + eps)

2. categorical_sample samples from pmf:

def categorical_sample(probs, n_samples):
    return np.random.choice(len(probs), size=n_samples, p=probs)

3. gumbel_max_sample performs the gumbel-max trick for the sampling

def gumbel_max_sample(logits, n_samples):
    # Expand logits to match the number of samples
    logits_expanded = np.tile(logits, (n_samples, 1))
    
    # Generate Gumbel noise
    gumbel_noise = sample_gumbel(logits_expanded.shape)
    
    # Add noise to logits and get argmax
    perturbed_logits = logits_expanded + gumbel_noise
    samples = np.argmax(perturbed_logits, axis=1)
    
    return samples

We can easily sample using both ways as fallows:

# Set parameters
logits = np.array([2.0, 0.5, 0.5, 1.0, 0.3])
n_samples = 10000
probs = softmax(logits)

# Generate samples using both methods
gumbel_samples = gumbel_max_sample(logits, n_samples)
categorical_samples = categorical_sample(probs, n_samples)

# Compute histograms
gumbel_hist = np.bincount(gumbel_samples, minlength=len(logits)) / n_samples
categorical_hist = np.bincount(categorical_samples, minlength=len(logits)) / n_samples

Here are the resulting histograms comparing both sampling methods:

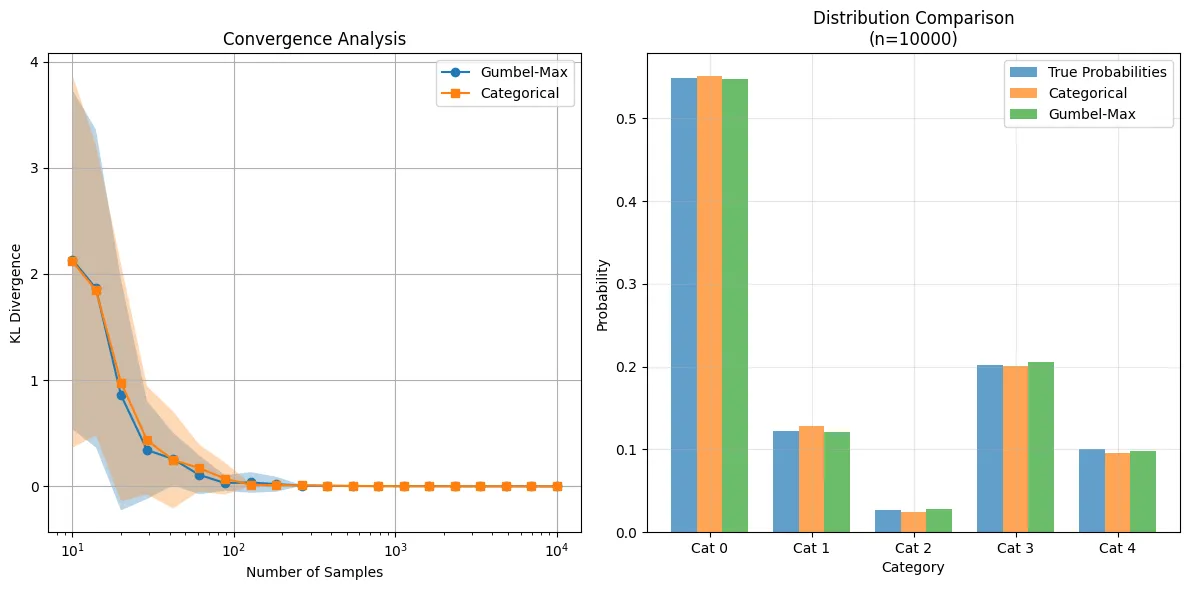
The notebook I use to plot the histograms are on my github

A* Sampling

The Gumbel-Max trick is also closely connected to A Sampling*, a method introduced in the paper titled “A* Sampling” by Maddison, Tarlow, and Minka (2014). In this paper, the authors propose a way to generalize the Gumbel-Max trick to handle sampling from continous distributions. They do so by, introducing the concept of a Gumbel process—a stochastic process where each point in a continuous domain is associated with a Gumbel random variable and by using A* search algorithms, they efficiently sample from complex continuous distributions.

This method has been instrumental in deep learning research, particularly in the development of the Gumbel-Softmax estimator (a.k.a. the Concrete distribution), which enables differentiable sampling from discrete distributions.

Extending to the Gumbel-Softmax Trick

I will extend the Gumbel-max trick to Gumbel-Softmax trick in another blog-post.

References

• Maddison, C. J., Tarlow, D., & Minka, T. (2014). A* Sampling. arXiv
• Maddison, C. J., Mnih, A., & Teh, Y. W. (2016). The Concrete Distribution: A Continuous Relaxation of Discrete Random Variables. arXiv
• Jang, E., Gu, S., & Poole, B. (2016). Categorical Reparameterization with Gumbel-Softmax. arXiv